Think of the solution as 2-stage process:

1. Construct a function that models the objective of the given problem (i.e., the objective function)

2. Find the absolute maximum (or minimum) of that function.

 

---

Illustration

The Pepsi co. wants to minimize the cost of materials it uses to package 12 oz cylindrical cans of beverage. Find the optimal dimensions of the can.

Solution outline:

Stage1:	Build the objective function. Always make a sketch here.
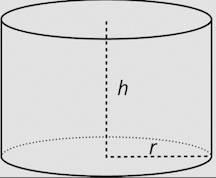
	Use unit conversion: 12 oz = 0.0125 ft\(^3\) Minimum material cost ==> minimum surface area. \(S(r) = 2\pi r h + 2 \pi r^2\)     (area of sides+top+bottom) Relate \(h\) to \(r\): \(~~\pi r^2 h = 0.0125\)     (since volume is known) \(S(r) = 0.025/r + 2\pi r^2\)
Stage2:	Use calculus to optimize.
	\(S^\prime(r) = -0.025/r^2 + 4\pi r\) Set \(S^\prime(r) = 0\) and find C.P.'s ==> \(r^3 = 0.025/(4 \pi)\) ==> \(r=0.1258\) ft. = 1.5 inches Show that it gives the absolute minimum. (How?) State the optimal dimensions: \(r =\ldots , h = \ldots\)

---

Illustration 2

A homeowner has 100 feet of fencing and wants to use it to enclose a rectangular garden. Find the dimensions of the largest garden it can enclose.

Solution outline:

Stage1:	(Objective function)
	Let \(x\)=length, \(y\)=width, of rectangle. Make a sketch. 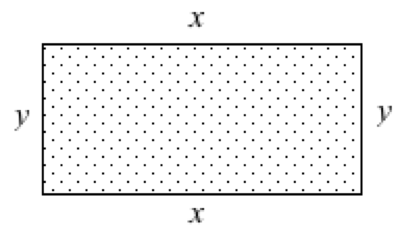Largest garden ==> maximize area. \(A(x,y) = x\cdot y\)     (area of garden) Relate \(y\) to \(x\): \(~~2 x + 2y = 100\) ft   (total length of fencing material) \(A(x) = x(100-2x)/2 ~ = x(50-x)\)
Stage2:	Use calculus to optimize.
	\(A^\prime(x) = (50-x) + x( -1) = 50 - 2x\) Set \(A^\prime(x) = 0\) and find C.P.'s ==> \(x = 50/2 = 25\) feet Show that it gives the absolute maximum. (How?) State the optimal dimensions: \(x =\ldots\) ft, \(y = \ldots\) ft

---